Path, Path space, evaluation and section function

Definition of Path function:

Mathematically, a path is a function of an interval $I$ to space $X$ where $I$ is from $[0,1]$. A path can also be a connection between some points in space $X$. To understand it more clearly, let's take an example of Global Positioning System(GPS). In GPS, when a person is finding a navigation between two points on a map, the result that comes out is the path between that two points. In topology, a path is a function defined by $\alpha : I \to X$ where the initial point is $\alpha(0)=a$ and the final point is $\alpha(1)=b$ as shown in Figure 1.

Figure 1(a): Simple example of a path between a and b

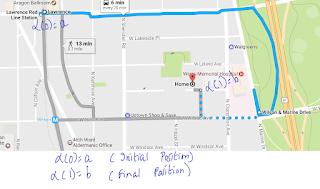Figure 1(b): Path in $GPS$

 Figure 1: Examples of different path

Definition of Path Space($PX$):

Path Space is a space which contains all the path in space $X$. It is written as:

$$PX=\{ \alpha \mid \alpha \, \mbox{is a path in} \, X \} $$

Definition of Evaluation function:

The evaluation function is the function which takes a path from the path space $PX$ as an input and gives a pair of initial and final position in the Cartesian Product $X \times X$ as an output. In other words, it is a function whose domain is the path space $PX$ and the codomain is the Cartesian Product $X \times X$. It is written as:

$$ev: PX \to X \times X $$

If we take a path as an input, then the output is the initial and the final position is shown in the Cartesian Product. For example, if $\alpha$ is the path taken as an input, then the output is the initial point $\alpha (0) $ and final point $\alpha (1)$ of that path.  

Definition of Section Functions:

The section is a one-sided inverse of the evaluation function because it takes two points on the Cartesian product as an input and gives a path between that two points as an output. It is written as:

$$s: X \times X \to PX \, \mbox{such that} \, ev \circ s= identity $$

This function is the main function in defining our motion planning problem as it takes two points and gives us the path between them, and that is what we need to move a robot from one position to another. To solve the motion planning problem means to find the section. The section can be continuous or discontinuous or may not exist. 

Identity Function:

First, you take two points as an input as of section and that gives you the path $\alpha$ between them. Second, we take that path $\alpha$ as an input as of evaluation function and it gives us the initial and final points. Therefore, these two functions give us the identity function. 

Posted by Chintan Patel.