By Watheq Al-Bnosha


For $8\times 8$ I got two shapes

the first shape I got was by dividing $8$ into two circles and multiply each circle by $8$ as it is shown in Figure 1.

                                                                           Fig. 1

we can imagine it like four torus on top of each other and the figure $8$ is in every single point of those torus, as we see in Figure 2.

                                                         
                                                                          Fig. 2

 The second shape I got was by moving the figure $8$ around every point in the other $8$,  as we see in Figure 3.

                                                                         Fig. 3 

Path, Path space, evaluation and section function

Definition of Path function:

Mathematically, a path is a function of an interval $I$ to space $X$ where $I$ is from $[0,1]$. A path can also be a connection between some points in space $X$. To understand it more clearly, let's take an example of Global Positioning System(GPS). In GPS, when a person is finding a navigation between two points on a map, the result that comes out is the path between that two points. In topology, a path is a function defined by $\alpha : I \to X$ where the initial point is $\alpha(0)=a$ and the final point is $\alpha(1)=b$ as shown in Figure 1.

Figure 1(a): Simple example of a path between a and b

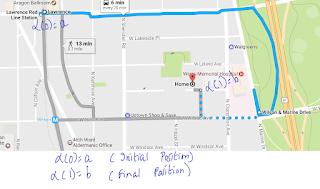Figure 1(b): Path in $GPS$

 Figure 1: Examples of different path

Definition of Path Space($PX$):

Path Space is a space which contains all the path in space $X$. It is written as:

$$PX=\{ \alpha \mid \alpha \, \mbox{is a path in} \, X \} $$

Definition of Evaluation function:

The evaluation function is the function which takes a path from the path space $PX$ as an input and gives a pair of initial and final position in the Cartesian Product $X \times X$ as an output. In other words, it is a function whose domain is the path space $PX$ and the codomain is the Cartesian Product $X \times X$. It is written as:

$$ev: PX \to X \times X $$

If we take a path as an input, then the output is the initial and the final position is shown in the Cartesian Product. For example, if $\alpha$ is the path taken as an input, then the output is the initial point $\alpha (0) $ and final point $\alpha (1)$ of that path.  

Definition of Section Functions:

The section is a one-sided inverse of the evaluation function because it takes two points on the Cartesian product as an input and gives a path between that two points as an output. It is written as:

$$s: X \times X \to PX \, \mbox{such that} \, ev \circ s= identity $$

This function is the main function in defining our motion planning problem as it takes two points and gives us the path between them, and that is what we need to move a robot from one position to another. To solve the motion planning problem means to find the section. The section can be continuous or discontinuous or may not exist. 

Identity Function:

First, you take two points as an input as of section and that gives you the path $\alpha$ between them. Second, we take that path $\alpha$ as an input as of evaluation function and it gives us the initial and final points. Therefore, these two functions give us the identity function. 

Posted by Chintan Patel. 

Introduction to robotics in topology, and defining the physical and configuration spaces

Robots are a machine which is programmed by an engineer using a computer to perform a task/s. When we tell a robot to perform certain task/s, the rules that we create for the robots to perform that tasks are called algorithm.

Now, let's look at the terms that we will use in understanding the basics of Topological Robotics.

Physical Space($\Gamma$):

Physical Space is the space where the robot/s will be performing their tasks. It is denoted as $\Gamma$. For example, as shown in Figure 6, if a robot is moving around the circle, then the physical space $\Gamma$ of that robot will be a circle $S^1$. 

Configuration Space:

• Configuration space is a space where you can abstractly define the position of robots and remove all the points where the robots cannot move which will help us to create an algorithm. 
• Mathematically, if we have $n$ robots moving on a Physical space $\Gamma$, then the configuration space will be:

$$C^n(\Gamma)= \Gamma \times \Gamma \times \Gamma \times \cdots \times \Gamma - \Delta$$ where $$\Delta= \{(x_1, x_2, x_3, \cdots,x_n) \mid \exists \, i \neq j \, where\, x_i=x_j \} $$

• The configuration space $C^1(\Gamma)$ of a robot moving on any physical space $\Gamma$ will always be $\Gamma$ because there is no cartesian product and diagonal as there is only one robot. 

Now, we will go through four examples of these two spaces.

1. A robot moving on an interval $I$.
2. Two robots moving on an interval $I$.
3. A robot moving on a circle $S^1$.
4. Two robots moving on a circle $S^1$.

A robot moving on a physical space $I$

• The configuration space $C^1(I)$ will only be $I$ as there is only one robot moving in that space. The Figure 1 showing the physical and configuration space(both are same):

Figure 1: Physical and Configuration space of a robot moving on $I$

Two robots moving a physical space $I$

• The configuration space $C^2(I)$ will be:

$$C^2(I)= I\times I- \Delta$$ where $$\Delta = \{ (x,y) \in I\times I\mid where\,  x=y\} $$

• Physical space is shown in Figure 2 and configuration space is shown in Figure 3.
• Here, the configuration space is divided into two different parts because of the diagonal $\Delta$.
• Therefore, we cannot interchange the position of the robots.

For example:

• Figure 4 shows that initial and final position of two robots moving on the $I$. 
• If we show that two positions in the configuration space, we can see from Figure 5 that it is impossible. The reason behind it is that the configuration space is divided into two spaces. 

Figure 2: Physical Space of two robots moving on $I$

Figure 3: Configuration space of two robots moving on $I$

Figure 4: Initial and Final Position of two robots moving on $I$ 

Figure 5: Initial and final position shown in the configuration space

A robot moving in a physical space $S^1$

• The configuration space $C^1(S^1)$ will be an $S^1$ as there is only one robot moving on the space. Figure 6 represents the physical and the configuration space:

Figure 6: Physical and Configuration space of a robot moving on a $S^1$

Two robots moving in a physical space $S^1$

• The configuration space $C^2(S^1)$ for this problem is: $$C^2(S^1)= S^1 \times S^1 - \Delta$$ where $$\Delta = \{ (x,y) \in S^1\times S^1\mid where \, x=y \} $$.
• We know that the cartesian product $S^1 \times S^1$ will be a torus as shown in Figure 8. But, for the configuration space, we will also have to remove the position of the robot where both overlap. 
• The physical and the configuration space is shown in Figure 7 and 9 respectively.
• Here, the configuration space is a two folded Mobius strip.
• Figure 10 shows the points where the $\Delta$ lies. 

Figure 7: Physical Space of two robots moving on a $S^1$

Figure 8: $S^1 \times S^1$ gives us torus

Figure 9: Configuration space of two robots moving on $S^1$ after cutting the $\Delta$

Figure 10: Line showing the $\Delta$

Posted by Chintan Patel.

Cartesian Product of a number 8 to a circle

$S^1\times 8$, if 8 intersects, then it is  going to give us the shape bellow

if 8 is like two circles in top of each others, then it is going to give us this shape

Watheq Al-Bnosha

Configuration Space for Two Robots on a Circle

The Scenario

Physical space $\Gamma =  S^1$ with the two robots $x$ and $y$

    Given the scenario of two robots on a physical space $\Gamma = S^1$ where the robots cannot overlap, what is the configuration space $X$?

Solution

    One can approximately define the configuration space $X$ as a Cartesian product of the physical space $\Gamma$ and itself by the number of robots. For example, if there were three robots in a physical space $\Gamma$, then the configuration space $X$ would approximately be $\Gamma \times \Gamma \times \Gamma$. The Cartesian product only approximates the configuration space since a diagonal $\Delta$ exists in the configuration space where the robots $x$ and $y$ overlap. The configuration Space then would be defined by the Cartesian product of the physical space minus the diagonal. When the physical space $\Gamma = S^1$, the configuration space $X$ is defined by:

$X = C^2 (\Gamma) = S^1 \times S^1 - \Delta$

    The diagonal $\Delta$ is just a set of points where $x$ and $y$ overlap and can be defined as:

$\Delta = \{(x,y) \in S^1 \times S^1 | x=y\}$

    What exactly does $X$ look like, though? $S^1 \times S^1$ is a torus, but since points that lie on the diagonal cannot exist in the configuration space, $X$ is a torus with a cut made along the diagonal. What shape does this make?

A torus or $S^1 \times S^1$

    One could also express the torus as a two-dimensional sheet where the opposite edges connect. Representing $X$ is as follows:

This drawing expresses $X$. The rectangle is a sheet where the edges that have a matching number of arrows connect to form the shape of a torus; the dashed line is the diagonal $\Delta$ where there is a cut in the torus; any point $(x,y)$, in the space that does not lie on $\Delta$, correlates to a valid configuration of the two robots in the physical space $\Gamma$ 

    Since the edges of the rectangle with a matching number of arrows denotes a connection and the dashed line denotes a cut along $\Delta$, then you could cut the rectangle along the dashed line and connect a pair of matching edges, resulting in the following:

    This then shows that the configuration space $X$ is a cylinder or $S^1 \times I$ where $I = [0,1]$.

- Luis Chirinos Discua

Homology, by HC

Check out this talk by Gunnar Carlsson (Stanford University):

Homology

Cartesian Products

   

                                                  Cartesian Products

                                                        September 11

                                                By Watheq Al-Bnosha

Introduction:

Cartesian Product is the combination of all ordered pairs of two series, such that each element of the first series  goes with all of the elements of the second series. For example, if we have two series $A$ and $B$. $A$ contains (1,3,5), and $B$ contains (2,4), so $A\times B$= {($A\times B$)| $A$∈$A$ and $Y$∈$Y$}

As shown in Fig.1

Fig. 1

Topologically, we can get many shapes when applying Cartesian products. For example, we get a torus when we multiply two circles which means that every point in the first circle is multiplied by every single point of the second circle to form the torus. $S^1\times S^1$

As it it shown in Fig.2

Fig. 2

And we get a cylinder by multiplying $I$\times $S^1$

^{where $I$ is just a straight line that goes from 0_________1}

Fig.3

Cartesian Product and its importance in the field of Topological Robotics

In this post, I will be talking about the basics of the Cartesian Product from the viewpoint of Set Theory and how can we use its idea in Topological Robotics. So, let's start with the basic definitions of Cartesian Product and see some examples to better grasp it meaning.

Cartesian Product:

Symbolically, Cartesian Product is written as $ A \times B$. It is a set of pairs of $x$ and $y$, where $x$ belongs to set $A$ and $y$ belongs to set $B$. Mathematically, it is written as: $$ A \times B= \{(x,y) \mid x \in A, y \in B\} $$

Let's see some examples and then we can start looking at Cartesian Products in Topology.

Example 1:

Suppose we have set $A=\{ 1, 2, 8 \}$ and set $B=\{ a, b \}$. Find $A\times B$.

The answer to this problem is:

$$A\times B=\{(1,a), (1, b), (2, a), (2, b), (8, a), (8, b) \} $$

Here, we can also say that Cartesian product $A\times B$ maps all elements of $A$ to the elements of $B$. 

Example 2:

Set $A= \{ a, b, m, n \}$ and set $B= \{1 \}$. Find $B\times A$.

$$ B\times A= \{(1,a), (1, b), (1, m), (1, n) \} $$

This proves that Cartesian Product is not a commutative property when looked at in terms of Set Theory. 

Now, let's think about how Cartesian Products can be used in Topology. If we look at the Cartesian Product used in last two examples, we can see that we map elements of one set to elements of another set or we can say that we had pairs of elements. In Topology, instead of mapping elements with elements, now we will map some interval with interval or some object with other objects. Let's dive into some problems to understand it more clearly.  

Example 3:

Find the Cartesian Product $I \times I$ where $I=[0,1]$. Solve the product and show it in Cartesian Coordinates. 

The answer for this is:

$$I\times I= \{(x, y)\mid where\, x\in [0,1] \, and \, y\in [0,1] \} $$

Example 4:

Find the Cartesian Product $I \times S^1$ where $I=[0,1]$ and $S^1$ is a circle. Solve the product and show it in Cartesian Coordinates. 

$$I\times S^1= \{(x,y)\mid where \, x\in I\, and \, y\in S^1 \} $$

Example 5:

Find the Cartesian Product $S^1 \times S^1$ where $S^1$ is a circle. Solve the product and show it in Cartesian Coordinates. 

$$S^1\times S^1= \{(x,y)\mid where \, x\in S^1 and \, y\in S^1\} $$

Example 6:

Find the Cartesian Product $I \times T$ where $T$ is an alphabet. Solve the product and show it in Cartesian Coordinates. 

$$I\times T= \{(x,y)\mid where \, x\in I\, and \, y\in T \} $$

Example 7:

Find the Cartesian Product $I \times Y$ where $Y$ is an alphabet. Solve the product and show it in Cartesian Coordinates. 

$$I\times Y= \{(x,y)\mid where \, x\in I \, and \, y\in Y\} $$

Example 8:

Find the Cartesian Product $I \times M$ where $M$ is an alphabet. Solve the product and show it in Cartesian Coordinates. 

$$I\times M= \{(x,y)\mid where \, x\in I\,  and\,  y\in M\} $$

Example 9:

Find the Cartesian Product $T \times S^1$. Solve the product and show it in Cartesian Coordinates.

$$T\times S^1= \{(x,y)\mid where \, x\in T\,  and\,  y\in S^1\} $$

Example 10:

Find the Cartesian Product $S^1 \times Q$ where $Q$ is an alphabet. Solve the product and show it in Cartesian Coordinates. 

$$S^1\times Q= \{(x,y)\mid where \, x\in S^1 and\,  y\in Q\} $$

Example 11:

Find the Cartesian Product $Q \times Q$. Solve the product and show it in Cartesian Coordinates. 

$$Q\times Q= \{(x,y)\mid where \, x\in Q\, and \, y\in Q\} $$

Posted by Chintan Patel.

[NEEEDS FIX] Discussion:Cartesian Product on 3-Dimensional play of a set $A$ and $B$ for a Hyperrectangle

Cartesian Product of Two Sets for a Hyperrectangle 

By Justin Merchan

Abstract 

Our objective is to create a hyperrectangle by combining two sets of ordered pairs under the concept of a Cartesian product. There will be use triplets in order to apply this practice to a three-dimensional space. 

Introduction

Given two sets $A$ and $B$, where the set of ordered pairs in $A$ are connected by a line, as well as the set of $B$. When $A \times B$, we should get an hyperrectangle (also known as a rectangular prism) Fig. 1a. 

My Solution

Given set $A=\{\alpha,\beta\}$, where $\alpha$ and $\beta$ are represented by the triplets $\alpha=(1,0,0)$ and $\beta=(1,2,0)$; times the set $B=\{a,b,c,d\}$, where $a,b,c,d$ are represented by the triplets, $a=(1,0,0)$; $b=(6,0,0)$; $c=(1,0,-4)$; and $d=(6,0,-4)$. 

Therefore, $A \times B=\{(\alpha,a);(\alpha,b);(\alpha,c);(\alpha,d);(\beta,a);(\beta,b);(\beta,c)(\beta,d)\}$   Fig. 1b.

*Please share with us your answer and final graph if possible. This is an open discussion, so if you catch a mistake, have any question regarding any of the solutions, or you have any opinion in general please comment it.

Topology Exercise: The Apartment.

Topology Exercise: The Four-Floor House

By Justin Merchan

Abstract

The objective of this example is to exercise our ability to analyze, visualize and solve problems that involve certain area by applying concepts of topology and the manipulation of areas. This exercise is developed around the idea of a homotopy equivalence.

Introduction

We are given a four-floor house, that we will be calling $X$. Each floor has a stair that connects the superior floor with the one below itself, excluding the first and the terrace.

Exercise:
Given space $X$, what simple space $Y$ $\simeq$ $X$. 

Sketch of the four-floor house

*This exercise is inspired on the exercise described by John Redford in his YouTube video "A Homotopy Problem" (Link Below) that I also recommend to check if you liked this problem.

https://www.youtube.com/watch?v=IcckvyQEBI0

Homotopic and Homeomorphic Letters

TC with Letters

September 3, 2017
By Watheq Al-Bnosha

Introduction

Homotopy and Homeomorphism apply to many objects and shapes. In this paper, we are going to apply homotopy and homeomorphism to letters and study which letters are homotopic, homeomorphic, and/ or neither. We are going to put in consideration the way a letter is written on different computers and handwriting.

The English alphabet are $ A, B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V,W,X,Y,Z. $

Homotopic Letters

In homotopy, dimensions do not matter. What matters is that we cannot glue or cut the shape of the letters or any other shape in general. But instead, we can compress and stretch the shapes. We are going to define the English alphabet into three sections depending on the holes they have.

1. $ A \simeq D, P, O, R, $ and $Q$. Because all of them have holes and if we compress or stretch them, they’ll look like the same.
2. $B$ would be by itself because it has two holes on it and there is no other letter with two holes.
3. $C \simeq E,F,G,H,I,J,K,L,M,N,S,T,U,V,W,X,Y,Z.$ Because if we compress or stretch them, they’ll look like the same.

Homeomorphic Letters

In homeomorphism, we have only 1-dimension. Also, we cannot compress or stretch letters We are going to use a technique to define the letters that are homeo to each other and the letters that are not homeo. In case there is a letter that is suspicious whether is homeo or not, we are going to choose a point in the letter and cut it. If the letter has the same points as the other one, then it is homeo, if it doesn’t then it is not homeo. We are going to put the English letters into seven sections depending on their dimensions.

1. $ H \approx I$. Because if we choose a point in a letter $H$ and cut it, it will have the same amount of pieces as the letter $I$ when we choose to a point and cut it.  
2. $C \approx L, N, S, U, V, G, Z, W, \, and M.$ We do not have to choose a point with these letters because they are one piece only. 
3. $D \approx O.$ 
4. $J \approx T, F, Y, \, and E.$ 
5. $K \approx X$. Each one will be four pieces when we choose a point in the middle and cut it. 
6. $P \approx Q.$ Both have circles and a leg.  
7. $B, R,$ and $A$ are unique. These three letters are not going to have equal pieces when cutting them.